协方差矩阵时机器学习中常用的概念,今天我们就来完整的介绍一下协方差和协方差矩阵的定义,以及使用python中的numpy包来实现。
一、协方差定义及公式
涉及到的相关概念:
- 期望
- 方差
- 协方差
<1>. 期望
设随机变量 只取有限个可能值
, 其概率分布为:
, 则
的数学期望,
为:
<2>. 方差
设 为随机变量,分布为
,则
或分布
的方差为:
,方差和标准差是刻画随机变量在其中心位置附近散布的数字特征。
统计学中对于样本方差的估计为: ,当样本量很大时,
接近于
<3>. 协方差
协方差用来刻画两个随机变量 ,
之间的相关性
如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
协方差的公式如下:
方差就是协方差的一种特殊形式,当两个变量相同时,协方差就是方差了。
<4>. 协方差矩阵
协方差矩阵就是很多个变量两两之间的协方差,构成的矩阵,即:
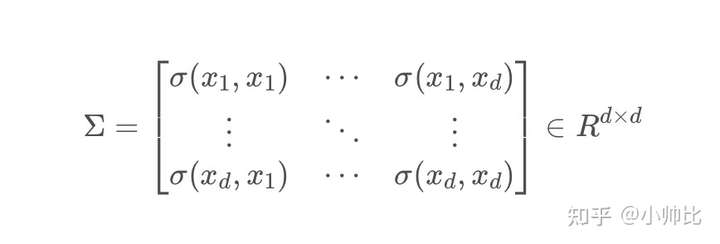
从上式可以看出,协方差矩阵中对角线上元素就是各个随机变量的方差,非对角线上的就是两两随机变量之间的协方差。
import numpy as np
import matplotlib.pyplot as plt#各取500个标准正态分布的数据
x1=np.random.normal(0,1,500)
x2=np.random.normal(0,1,500)#将x1,x2以向量的形式排列起来
X=np.vstack((x1,x2)).T#计算协方差
def cov(x1,x2):
x1mean,x2mean=x1.mean(),x2.mean()
Sigma=np.sum((x1-x1mean)*(x2-x2mean))/(len(x1)-1)
return Sigma#协方差矩阵
def covMatrix(X):
matrix=np.array([[cov(X[0],X[0]),cov(X[0],X[1])],[cov(X[1],X[0]),cov(X[1],X[1])]])
return matrixcovMatrix(X)
# #output
# ”’
# array([[0.00437243, 0.0433571 ],
# [0.0433571 , 0.42993022]])
# ”’### 解法2
a = np.array([[1,2,3],[3,1,1]])
print(np.cov(a))# # output
# array([[1,-1],
# [-1,1.33]])