matlab 官方解释
地址:箱线图 – MATLAB boxchart – MathWorks 中国
箱线图为数据样本提供汇总统计量的可视化表示。对于给定数值数据,对应的箱线图显示以下信息:中位数、下四分位数和上四分位数、任何离群值(使用四分位差计算得出)以及不是离群值的最小值和最大值。
- 每个箱内的线条表示样本中位数。您可以使用
median函数计算中位数的值。 - 每个箱的上边缘和下边缘分别表示上四分位数和下四分位数。顶部和底部边缘之间的距离表示四分位差 (IQR)。有关如何计算四分位数的详细信息,请参阅
quantile,其中上四分位数对应 0.75 分位数,下四分位数对应 0.25 分位数。 - 离群值是指距离箱顶部或底部超过 1.5 · IQR 的值。默认情况下,
boxchart使用'o'符号显示每个离群值。离群值的计算方式与在'quartiles'方法中使用isoutlier函数类似。 - 须线是延伸到每个箱的上方和下方的线条。一条须线将上四分位数与最大非离群值(不是离群值的最大值)相连,另一条须线将下四分位数与最小非离群值(不是离群值的最小值)相连。
- 缺口有助于您比较多个箱线图中的样本中位数。当您指定
'Notch','on'时,boxchart函数会在每个中位数周围创建锥形着色区域。在 5% 显著性水平上,缺口不重叠的箱线图具有不同中位数。显著性水平基于正态分布假设,但对于其他分布而言,中位数比较相当稳健。缺口区域的顶部和底部边缘分别对应于 m+(1.57⋅IQR)/√n 和 m−(1.57⋅IQR)/√n,其中 m 是中位数,IQR 是四分位差,n 是数据点数,不包括NaN值。

指定 'Notch','on',这样每个箱都包括一个称为缺口的锥形着色区域。在 5% 显著性水平上,缺口不重叠的箱线图具有不同中位数。
——————————
为方便理解,搜集的民间解释:

患者的中位数年龄为 39 岁,如箱内的线条所示。32 岁和 44 岁的下四分位数和上四分位数分别显示为箱的底部和顶部边缘。须线(即在框下方和上方延伸的线条)的端点对应于最年轻和最年长的患者。年龄最小的患者是 25 岁,最大的是 50 岁。数据集不包含由小圆圈表示的离群值。
第一四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
第三四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range,IQR)
箱线图与正态分布关系


- 中位数(Q2 / 50th百分位数):数据集的中间值;
- 第一个四分位数(Q1 / 25百分位数):最小数(不是“最小值”)和数据集的中位数之间的中间数;
- 第三四分位数(Q3 / 75th Percentile):数据集的中位数和最大值之间的中间值(不是“最大值”);
- 四分位间距(IQR):第25至第75个百分点的距离;
- 晶须(蓝色显示)
- 离群值(显示为绿色圆圈)
- “最大”:Q3 + 1.5 * IQR
- “最低”:Q1 -1.5 * IQR
离群值
| 离群值 离群值(outlier)也叫异常值,简单来说就是与其他数据点明显不同的测量值。在箱形图中: 大于上四分位数+1.5倍四分位间距的值或者小于下四分位数-1.5倍四分位间距的值被定义为离群值。 大于上四分位数+3倍四分位间距的值或者小于下四分位数-3倍四分位间距的值被定义为极端离群值(extreme outliers)。 离群值对一些统计量影响很大(比如均值),因此有时需要留意。 离群值的处理 发现离群值后有几种常用方法可以减少离群值对分析的影响。在应用这些方法前需要先检查一下离群值是否是数据错误录入造成。如果数据录入无误,主要有三种处理方法: 剔除离群值:当有理由认为该样本不属于目标总体时可以采用这种方式。 数据转换 更改测量值 常见更改测量值的方法: (1)用次高或次低的测量值替代 (2)用Z分数反推出替代值 Z值大于3.29也是判定离群值的一种方法。据此可以反推Z值为3.29时对应测量值应该是多少: 可用该值替代离群值 (3)用均值加或减2倍标准差替代 |
第一件事情,不是所有的数据都适合画箱线图,不信,请看学生画的丑图。
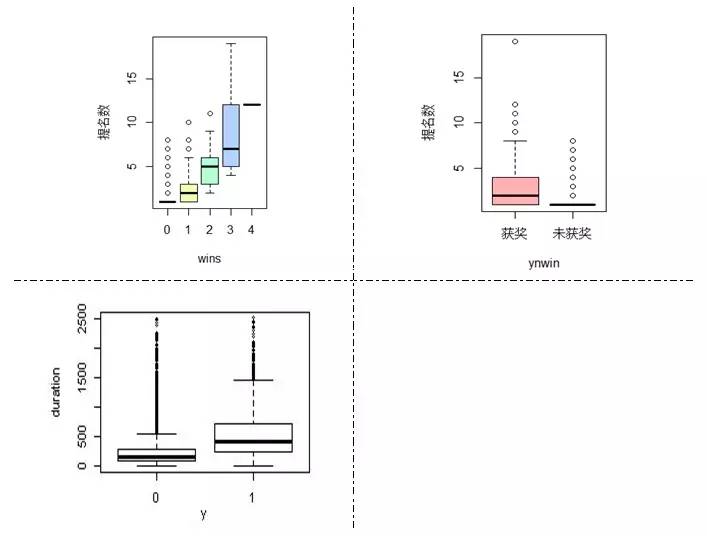
图2 丑图示例
这几组箱线图看着不舒服,主要原因是,箱子被压得很扁,甚至只剩下一条线,同时还存在着很多刺眼的异常值。这种情况的出现,有两个常见的原因。第一是,样本数据中,存在特别大或者特别小的异常值,这种离群的表现,导致箱子整体被压缩,反而凸显出来这些异常;第二是,样本数据特别少,数据一少,就有可能出现各种诡异的情况,导致统计图长得对不起观众。
如果你画出的箱线图是这样的,那么有两个解决办法。第一,如果数据取值为正数,那么可以尝试做对数变换。对数变换水妈必须墙裂推荐,称得上画图界的整容神器,专治各种不对称分布、非正态分布和异方差现象等。图3就是整容前后的一组箱线图。你说我不想做变换,那么可以采取第二种解决办法,那就是,不画箱线图。

图3 对数变换前后的箱线图
以上是第一点要说明的,不是所有数据都适合画箱线图。第二点要说明的,更加重要的,那就是箱线图应该怎么用。答案是,配合着定性变量画分组箱线图,作比较!分组箱线图是水妈最喜欢的统计画图工具,没有之一。
如果只有一个定量变量,很少用一个箱线图去展示其分布,而是更多的选择直方图。箱线图更有效的使用方法,是作比较。我们举两个栗子。
第一个例子,我上课经常讲。假设我现在要比较男女教师的教学评估得分,用什么工具最好。答案是箱线图。没有比较就没有伤害,大家看图4能够明显感觉到箱线图是更有效的工具,能够从平均水平(中位数),波动程度(箱子宽度)以及异常值对男女教师的教学评估得分进行比较,而直方图却做不到。

图4 进行比较时,箱线图是更有效的工具
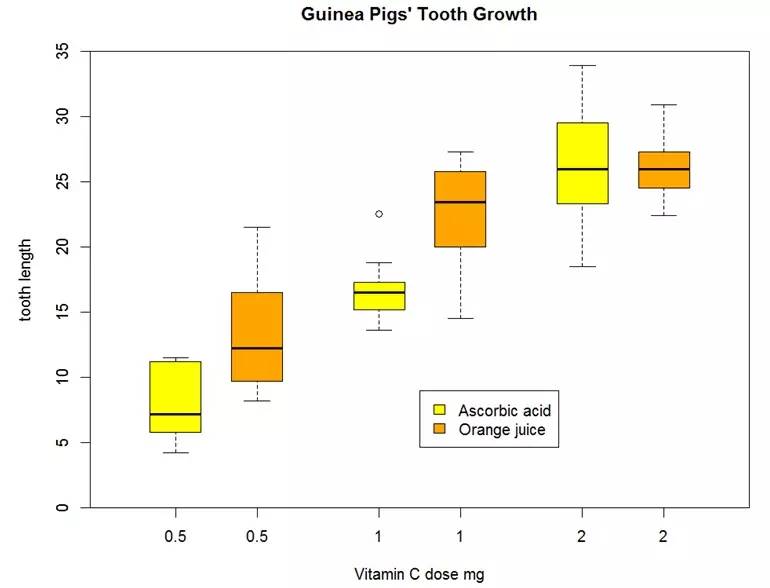
第二个例子,来自R语言里面的boxplot的example,水妈觉得很好看,拿来跟大家分享。这个箱线图略复杂,共涉及3个变量。定量变量是牙齿生长长度,体现在图形的纵坐标,也就是箱子展示的内容。第一个定性变量是维他命C的剂量,三个水平(0.5mg,1mg和2mg),体现在横坐标,所以一共有3组箱线图;第二个定性变量是食用的食物,是维C还是橙汁,分别用黄色和橙色展现,所以每组箱线图里又包含两个箱子。
如何正确理解箱线图(box plot)的含义 – 知乎 (zhihu.com)
对数变换与正态分布