误差棒选谁——SD，SE，SEM傻傻分不清？

转自：误差棒选谁——SD，SE，SEM傻傻分不清？ – 知乎 (zhihu.com)

先写阅读后结论：mean+-SD，表示离散程度；mean+-SEM表示精确度；用途不同，采用表达不同。

个人认为在一般科研中数据表示中，检测领域等，相对应表达精度。

下面为原文：

一、概念甄别

SD，标准差（Standard Deviation）：标准差是对数据集中每个数据值与其均值之间差异的一种度量，用来描述数据集的离散程度（data is distributed around mean）。标准差越大，表示数据集中的个体差异越大。平均数相同的两组数据，标准差未必相同。（图 1.1）

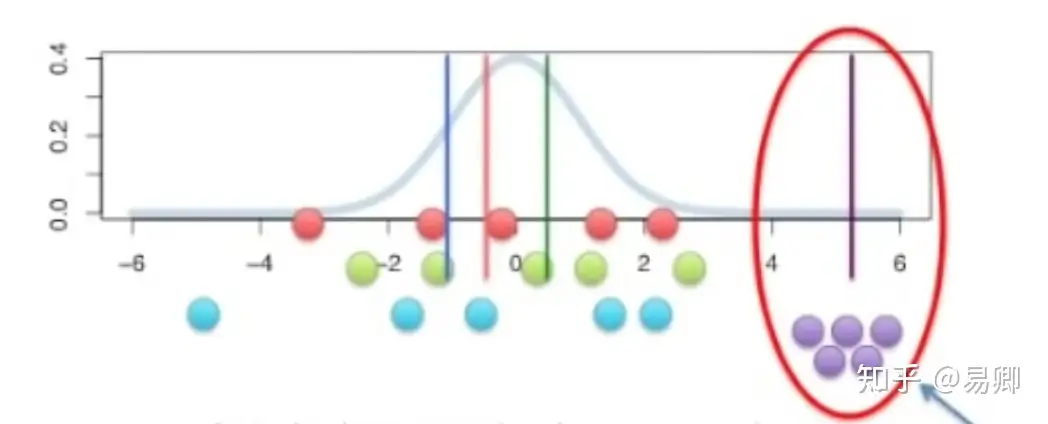
图 1.1 离散程度与可靠性的区别（红、绿、蓝、紫点代表不同次的抽样，相同颜色的竖线代表此次抽样的均值。由此可见，紫色次数抽样的时候，虽然本次的离散程度低，但是可靠程度并不高，但这种情况是罕见的）参考：https://statquest.org/the-standard-error-and-a-bootstrapping-bonus/

SEM，均值标准误（Standard Error of the Mean）：简称标准误（SE，standard error），也是样本均值估计值的标准差（how the mean is distributed）。标准误用来衡量抽样误差，标准误越小表明样本统计量与总体参数的值越接近，样本对总体更具有代表性，用样本统计量推断总体的参数的可靠程度越大。因此，均值标准误是统计推断可靠性的指标。但是它通常只用于描述样本的均值，而不是总体的均值。（图 1.2）

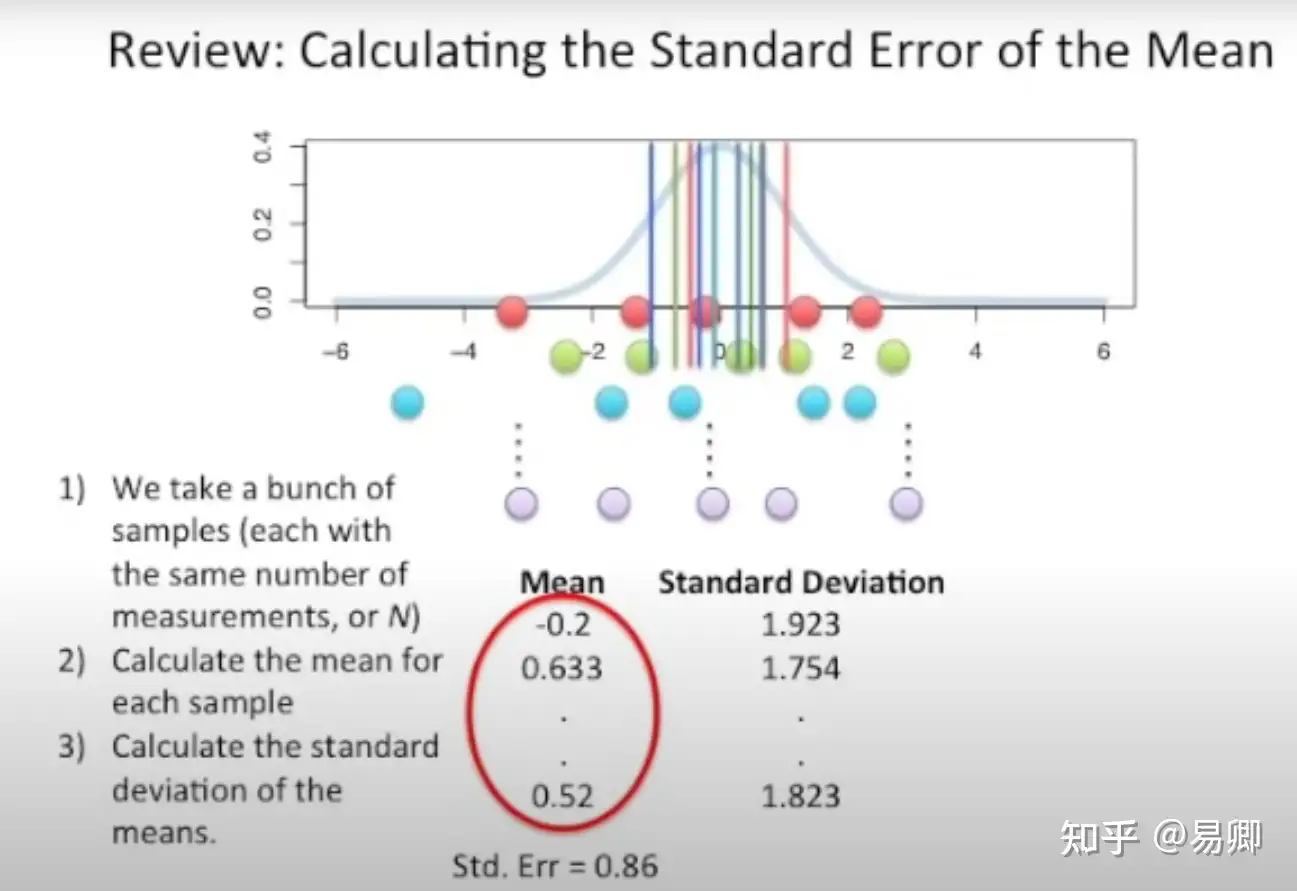
图 1.2 标准误的来源（计算的是均值的标准差，因为1个SD一般能覆盖68%的值，2个SD一般能覆盖95%的值。一般而言，SEM不会大于SD）参考：https://statquest.org/the-standard-error-and-a-bootstrapping-bonus/

另外，误差棒还有一种表现形式是置信区间（confidence intervals，CI），其与标准误有关。对于大样本（例如，大于10个），您可以使用以下经验法则：67%置信区间从平均值向每个方向延伸约一个SEM。95%置信区间从平均值向每个方向延伸约两个SEM。可参考：GraphPad Prism 9 Statistics Guide – 关键概念：SEM (graphpad-prism.cn)
除了常见的样本量𝑆𝐷÷样本量，SE还可以通过重抽样的方式获得（bootstrap）。可参考：The Standard Error (and a bootstrapping bonus!!!)

二、SEM和SD的选择

Mean±SEM：如果你希望强调样本均值的精确程度，可以使用SEM。一般推荐使用SEM，既能比较准确的估计均值，也能较好的反映数据置信区间。

Mean±SD：如果你希望强调数据的离散程度，可以使用SD。

SEM和SD的联系：在一个巨大样本的情况下，即使数据非常分散，使用SEM，您也能非常精确地知道平均值的值。
有一种说法是：对于重复数少的小样本（n≤30），考虑其离散度的可能，用mean ± S.E.M.，重复数多的大样本（n＞30）用 mean ± SD。可参考：mean ± S.E.M.和 mean ± SD有什么区别